Quaternions

Quaternions provide a clever way to encode a 3d rotation about a particular axis in 3d space. It is widely used in game mechanics and 3d computer aided designs.

A Quaternion is represented by 4 numbers (4 dimensions) which encodes a 3d rotation in 3d space.

q = a + i b + j c + d k

Imaginary Numbers??? Or vectors?

Recall how an imaginary number encodes a rotation. Let's define $i$ , $j$ , $k$ axis. Where $i$ represents a $90^{\circ}$ rotation about the $i$ axis and so on. Rotation is defined using the right hand rule, with the thumb pointing in the direction of the vector.

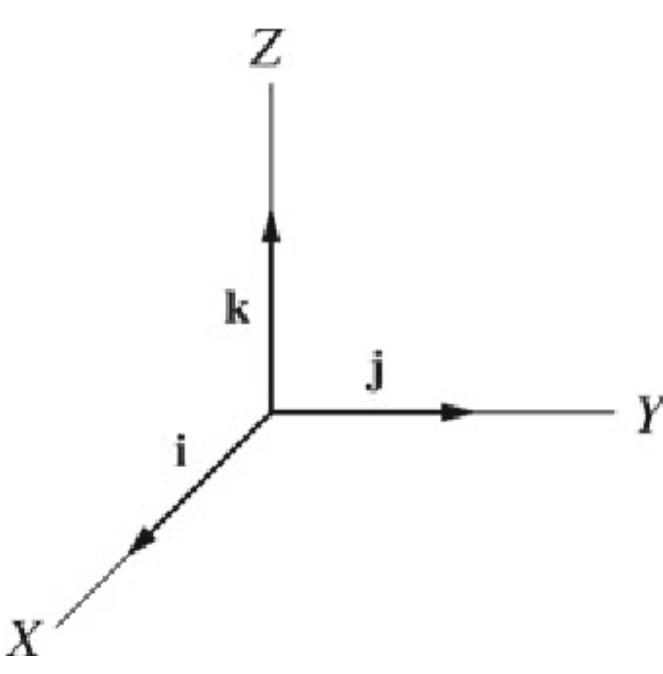
Let's define multiplication as such.

i j = k

This means applying a rotation $i$ on vector $j$ . Using your right hand, position the thumb in the direction of $i$ , and curl your fingers. $j$ will rotate according to the direction of the curl to become $k$ .

Doing so, you can derive other sets of expression. Like

\begin{array}{r} i j = k i k = - j \end{array}

Suppose we multiply $i$ on the left side of $i j$

i i j = i k = - j

Thus

i^{2} = - 1

We can also prove that

i^{2} = j^{2} = k^{2} = i j k = - 1

These are all imaginary numbers! What?? Note that $i \neq j \neq k \neq \sqrt{- 1}$ . Rather these are matrices that encode rotation.

\begin{aligned} i & = (\begin{array}{c} 0 & - 1 \\ 1 & 0 \end{array}) \end{aligned} j = (\begin{matrix} i & 0 \\ 0 & - i \end{matrix}) k = (\begin{matrix} 0 & i \\ i & 0 \end{matrix})

If you were to square the matrix, using matrix multiplication, you would obtain $(\begin{matrix} - 1 & 0 \\ 0 & - 1 \end{matrix}) = - i = - 1$ .

Why four dimensional space?

First of all, why would you introduce 4 dimensions, why can't a quaternion just be $q = a + i b + j c$ ?? See below.
Proof for 3d contradiction (Quaternions)

Conjugate

The conjugate of a quaternion is as such

q^{*} = a - i b - j c - k d

Thus

q \cdot q^{*} = a^{2} + b^{2} + c^{2} + d^{2} = | | q | |^{2}

Rotations

Let a $u$ be a pure imaginary quaternion or vector where $u \in H$ .
( $u$ is a quaternion).

u = i b + j c + k d = (\begin{matrix} b \\ c \\ d \end{matrix})

Where $b^{2} + c^{2} + d^{2} = 1$ .

A unit Quaternion existing on the surface of a hypersphere where $| | q | | = 1$ , can encode a rotation of $θ$ about unit vector $u$ .

q = \cos θ + u \sin θ

Where $q q^{*} = | | q | |^{2} = \cos^{2} θ - (u^{2}) \sin^{2} θ$ . Think of $u$ now as a vector

u^{2} = u \cdot u = - b^{2} - c^{2} - d^{2} = - 1

Thus $| | q | |^{2} = \cos^{2} θ + \sin^{2} θ = 1$ .

We can represent a unit quaternion by

q = e^{u \cdot θ}

The inverse of $q$ is

q^{- 1} = e^{- u \cdot θ} = \cos θ - u \sin θ = q^{*}

To rotate a vector $v$ about $u$ by $2 θ$ degrees.

v^{'} = q v q^{- 1}