Probability

Classical definition of Probability

Probability measures the likelihood of an event happening.

The classical definition of probability, also known as the Laplace definition, states that if an experiment has a finite number of equally likely outcomes, the probability of an event occurring is given by:

P (E) = \frac{Number of favorable outcomes}{Total number of possible outcomes}

Combined events

P (A \cup B) = P (A) + P (B) - P (A \cap B)

Independence Relation

if Event A and B are independent, then

P (A \cap B) = P (A) P (B)

Conditional Probability

$P (B | A)$ is the probability of $B$ occurring given that $A$ has already occured. We see that

P (A) \cdot P (B | A) = P (A \cap B)

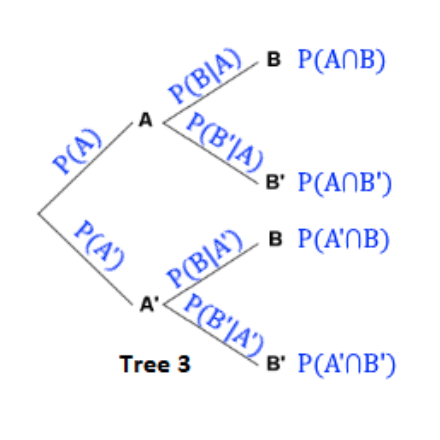
Thus

P (B | A) = \frac{P (A \cap B)}{P (A)}

P (A | B) = \frac{P (A \cap B)}{P (B)}

Bayes Theorem

Thus

P (A | B) = \frac{P (B | A) P (A)}{P (B)}

Since $P (B)$ can be rewritten as $P (B \cap A^{'}) + P (B \cap A)$ . Rearranging our conditional probability statement

P (A | B) = \frac{P (B | A) P (A)}{P (B | A^{'}) P (A^{'}) + P (B | A) P (A)}

Random Variables

Probability Mass Function (PMF)

It denotes the probability that a discrete random variable $X$ would equate to the value $x$ .

P (X = x)

Probability Density Function (PDF)

For continuous random variable, $P (X = x)$ is not meaningful as it would just be 0. For example, suppose a computer can randomly generate real numbers. It is impossible that it will output $x$ due to the uncountably infinite many other possibilities. However, its output can come ridiculously close to $x$ . And the probability that it is close to $x$ is defined by the probability density at $x$ .

f_{X} (x)

where $f_{X}$ is the probability density function which measures the probability that $X$ would be close to $x$ . More about them here

To find the probability that $a \leq X \leq b$

P (a \leq X \leq b) = \int_{a}^{b} f_{X} (x) d x

Expectation

The expectation function, reveals the expected value of X in the long term. It is the product of x and the probability of x occurring. #Expectation

Discrete:

E (X) = \sum_{x} x P (X = x)

Continuous:

E (X) = \int_{- \infty}^{\infty} x f_{X} (x) d x

Properties of Expectation

Constant

E (c) = c

Scalar Multiplicativity

E (a X) = a \cdot E (X)

Linearity of Expectation

E (X + Y) = E (X) + E (Y)

Product of Two independent Variables

If $X$ and $Y$ are independent

E (X \cdot Y) = E (X) \cdot E (Y)

Variance

Formula

Variance is the spread of the random variable $X$ from its mean $E (X)$ #Variance

V a r (X) = E (X - E (X))^{2}

We can also rewrite it as

\begin{aligned} V a r (X) & = E (X - E (X))^{2} \\ = E (X^{2} - 2 \cdot E (X) X + E (X)^{2}) \\ = E (X^{2}) - 2 \cdot E (X)^{2} + E (X)^{2} \\ = E (X^{2}) - E (X) \end{aligned}

$∴$

V a r (X) = E (X^{2}) - E (X) = σ^{2}

It can be equated to $σ^{2}$

Properties of Variance

Constant

V a r (c) = 0

Scalar Multiplicativity

V a r (c X) = c^{2} V a r (X)

Translation Invariance

V a r (X + c) = V a r (X)

Additivity

V a r (X + Y) = V a r (X) + 2 C o v (X \cdot Y) + V a r (Y)

If $X$ and $Y$ are independent, its covariance is 0. $∴$

V a r (X + Y) = V a r (X) + V a r (Y)

Cumulative distribution Function

Is the summation of the Probability Mass and Density function. It is an S-shaped curve

Discrete

F (x) = P (X \leq x) = \sum_{t \leq x} P (X = t)

Continuous

F (x) = P (X \leq x) = \int_{- \infty}^{x} f_{X} (t) d t

Look at Distributions

Binomial Distributions

E (X) = n p

E (X) = n p (1 - p)

Modern Axiomatic Definition

It is based on the Kolmogorov probability axioms. Which extends the definition to unequal probability distributions, and also probability with infinite outcomes.

Kolmogorov Probability Axioms

let $(Ω, F, P)$ be the measure space where
$Ω$ is the sample space (Set of all elements)
$F$ is the event space (Set of all events) $F = {E_{1}, E_{2} \dots}$
$P$ is the probability measure that outputs a probability of an event $E$

$P (E) \in R, P (E) \geq 0 \forall E \in F$
$P (Ω) = 1$
$P (⋃_{i = 0}^{\infty} E_{i}) = \sum_{i = 0}^{\infty} P (E_{i})$ if $E_{i}$ are disjoint