Linear Algebra

Linear Algebra (Elementary)

Vectors

Vectors are usually represented as column of numbers that encode a direction and magnitude.

\vec{v} = (\begin{matrix} x_{1} \\ x_{2} \\ ⋮ \\ x_{n} \end{matrix})

The magnitude of a vector can be determined by summing the square of each term in the column and square rooting the result.

| \vec{v} | = \sqrt{x_{1}^{2} + x_{2}^{2} + \dots + x_{n}^{2}} = \sqrt{\sum_{n = 1} x_{n}^{2}}

Dot Product

The Dot product of two vectors is

A \cdot B = | A | | B | \cos θ

And

A \cdot B = \sum_{n = 1} a_{n} b_{n}

Look at derivation of the formula here

Cross Product

The cross product of two vectors creates another vector that is perpendicular to both vectors.

A \times B = | A | | B | \sin θ \hat{n}

Where $\hat{n}$ is a unit vector perpendicular to A and B. The direction of $\hat{n}$ can be determined using the right hand grip rule.

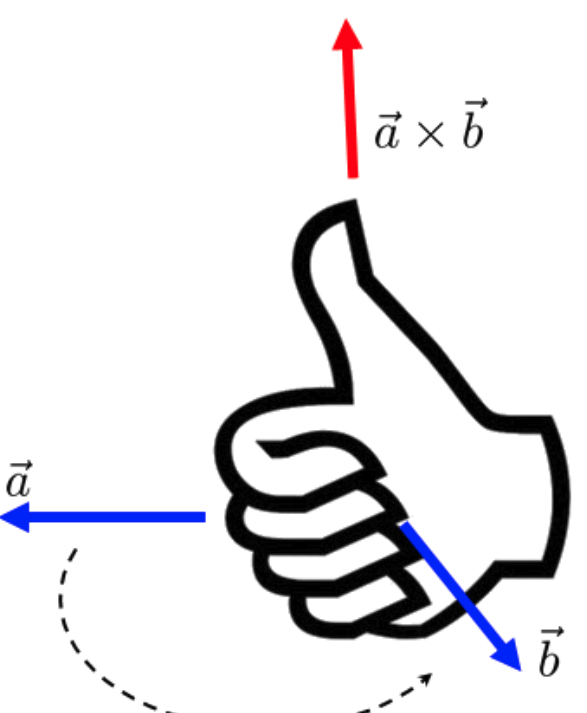
Your fingers curl from vector a to b, while your thumb represents the direction of $a \times b$

Thus

A \times B = - B \times A

The determinant trick to finding cross product.

(\begin{matrix} a_{1} \\ a_{2} \\ a_{3} \end{matrix}) \times (\begin{matrix} b_{1} \\ b_{2} \\ b_{3} \end{matrix}) = (\begin{matrix} a_{2} b_{3} - b_{2} a_{3} \\ - (a_{1} b_{3} - b_{1} a_{3}) \\ a_{1} b_{2} - b_{1} a_{2} \end{matrix})

Cover up the first row
Multiply both sides diagonally and subtract it. (First element)
Cover up second row
Multiply both sides diagonally and subtract it. Multiply by -1. (Second element)
Cover up third row
Repeat step 2 (third element)

Area bounded by Vectors

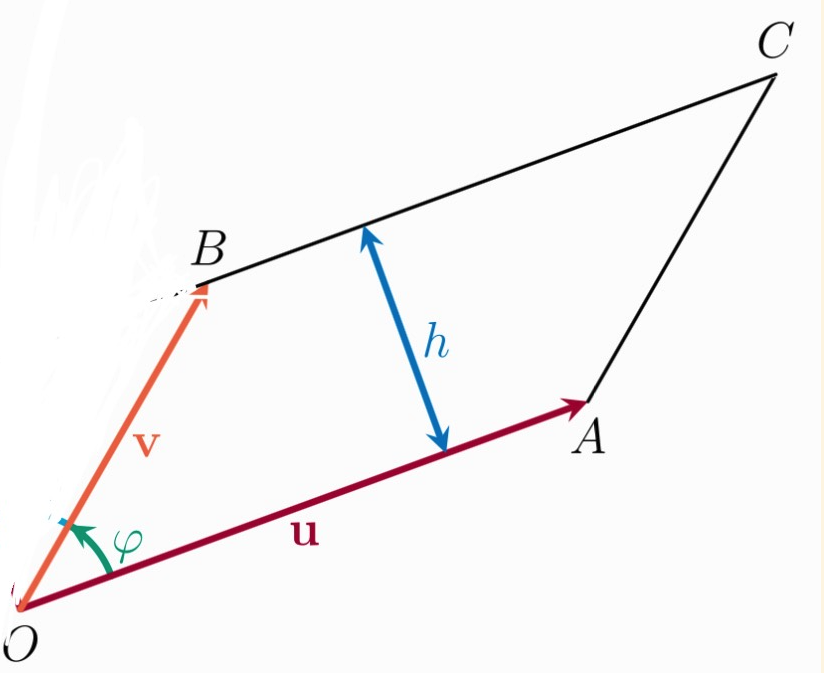
The area of the parallelogram can be deduced. Let $u$ be the base and $h$ be the height. The Area would be $| u | h$ . $h$ can be expressed as.

h = | v | \sin θ

Thus

| u | h = | u | | v | \sin θ = | u \times v |

Thus the area of the parallelogram can be determined by the magnitude of the cross product of $u$ and $v$ .

Sample qn: Prove that the volume of a cuboid is. (This result is widely used in determinants and cross products)

Volume of Cuboid = | a \cdot (b \times c) |

Points, Lines, Planes

Point

A point is self-evidently a point in 3d space.

Lines

Starting from what we know best

y = m x + b

A line in a vector space can be described as

\hat{r} = \hat{a} + t \hat{b}

Distance between Point and Line

The distance between $\hat{c}$ and $\hat{r} = \hat{a} + t \hat{b}$ is

d = \frac{1}{| | \hat{b} | |} | | (\hat{c} - \hat{a}) \times \hat{b} | |

Planes

Starting from what we know. The equation of a plane in Cartesian form is

a x + b y + c z = D

Using the properties of dot product, it can be rewritten as

(\begin{matrix} x \\ y \\ z \end{matrix}) \cdot (\begin{matrix} a \\ b \\ c \end{matrix}) = D

r \cdot \hat{n} = D

where $\hat{n}$ is the normal vector of the plane. And $r$ is a vector that lies on the plane

Line of Intersection between two planes

Given two planes

\begin{array}{r} x + y + z = 1 \\ 2 x + 3 y + z = 5 \end{array}

The line of intersection can be found by keying this into GDC (menu - 3 - 2)

Thus

\begin{aligned} x = - 2 z - 2 y & = z + 3 z = z \\ \frac{x + 2}{- 2} & = \frac{y - 3}{1} = z \\ (\begin{array}{c} x \\ y \\ z \end{array}) & = (\begin{array}{c} - 2 \\ 3 \\ 0 \end{array}) + λ (\begin{array}{c} - 2 \\ 1 \\ 1 \end{array}) \end{aligned}

Intersection of Planes

Given three planes ( $\prod_{1}, \prod_{2}, \prod_{3}$ ), the plane must intersect at a unique point when

n_{1} \cdot (n_{2} \times n_{3}) \neq 0

However, the planes has $0$ or $\infty$ solutions when

n_{1} \cdot (n_{2} \times n_{3}) = 0

Distinguishing between no solutions & Infinite solutions

! If $n_{1} \cdot (n_{2} \times n_{3}) = 0$ :

Find $l$ : the line of intersection between $n_{2}$ and $n_{3}$

l = (\begin{matrix} a \\ b \\ c \end{matrix}) + λ (n_{2} \times n_{3})

Check if the below condition is true. If yes, then $(a, b, 0)$ lies on $\prod_{3}$ , suggesting that there are infinite solutions. If not, there are no solutions

(\begin{matrix} a \\ b \\ c \end{matrix}) \cdot n_{1} = D_{3}

Distance between two parallel planes

where $D_{1}$ and $D_{2}$ are $r \cdot n = D_{1}$ and $r \cdot n = D_{2}$ .

d = \frac{D_{2} - D_{1}}{| | n | |}

Linearity

Formal definition of Linearity #Linearity

Additivity: $L (\vec{v} + \vec{w}) = L (\vec{v}) + L (\vec{w})$
Scaling: $L (c \vec{v}) = c L (\vec{v})$

Where $L$ is a linear transformation on a corresponding vector.

Matrices

Recall how a function in algebra transforms x to y?

f (x) = y

In linear algebra, instead of x and y's which are scalar values, linear algebra transforms vectors into another vector.

f (\vec{x}) = \vec{y}

However, to make the distinction clearer, mathematicians use A instead of f.

A \vec{x} = \vec{b}

We need special tools to work with vectors, and this is where matrices comes in. A matrix encodes a Linear transformation on a vector, similar to how a function (f) encodes a transformation of x to y.

eg.

(\begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix}) \hat{x} = \hat{y}

where A is a matrix and $A = (\begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix})$

(\begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix}) (\begin{matrix} x_{1} \\ x_{2} \end{matrix}) = (\begin{matrix} y_{1} \\ y_{2} \end{matrix})

Note that the dim of a vector has to be the same as the number of columns of matrix (A).

Matrix Multiplication (How does it transform between $\hat{x}$ to $\hat{y}$ ?)

Matrix multiplication

Take the nth row of numbers in A
Pivot it clockwise by 90 degrees into the mth column in $\hat{x}$
Multiply it respectively with the variable associated with it
Add up all the numbers in the column
The value would be on the nth row and mth column in $\hat{y}$

(\begin{matrix} a & b \\ c & d \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} a x + b y \\ c x + d y \end{matrix})

Thus

(\begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix}) (\begin{matrix} x_{1} \\ x_{2} \end{matrix}) = (\begin{matrix} x_{1} + 2 x_{2} \\ 3 x_{1} + 4 x_{2} \end{matrix})

Bravo!! We have transformed $\hat{x}$ into a completely new vector $\hat{y}$ !!

System of Linear Equations

A matrix also encodes a system of linear equations. Suppose there are 2 equations as shown, and we want to solve for a and b.

{\begin{cases} a + b = 20 \\ 2 a + b = 23 \end{cases}

A matrix representation of the above is as given

(\begin{matrix} 1 & 1 \\ 2 & 1 \end{matrix}) (\begin{matrix} a \\ b \end{matrix}) = (\begin{matrix} a + b \\ 2 a + b \end{matrix}) = (\begin{matrix} 20 \\ 23 \end{matrix})

look, aren't they equivalent??

Solving for the coefficients are as easy as

(\begin{matrix} a \\ b \end{matrix}) = {(\begin{matrix} 1 & 1 \\ 2 & 1 \end{matrix})}^{- 1} (\begin{matrix} 20 \\ 23 \end{matrix})

Where the inverse of the matrix is essentially the reverse of its transformation, similar to how $f : x \mapsto y$ , thus $f^{- 1} : y \mapsto x$ . Note, the inverse does not exist if the transformation is not one to one. But for square matrices, there is always an inverse 99% of the time.

Transpose

Transpose means to flip a vector or a matrix around a diagonal #Transpose

{(\begin{matrix} x_{0} \\ x_{1} \\ x_{2} \end{matrix})}^{T} = (\begin{matrix} x_{0} & x_{1} & x_{2} \end{matrix})

Thus

v^{T} v = v \cdot v

In the case of matrices

{(\begin{matrix} a_{00} & a_{01} & a_{02} \\ a_{10} & a_{11} & a_{12} \end{matrix})}^{T} = (\begin{matrix} a_{00} & a_{10} \\ a_{01} & a_{11} \\ a_{02} & a_{12} \end{matrix})

Another property is that $A^{T} A$ always result in a square matrix. As one matrix transforms a vector $m \times 1$ to $n \times 1$ , and the other transforms it from $n \times 1$ to $m \times 1$ . Together, the two transformation transforms a vector from $m \times 1$ to $m \times 1$ . Which is a property of a square matrix.

Determinant

Determinant measures the transformation of space and volume.

A matrix that maps basis vector $e_{1} . e_{2}, e_{3}$ to vectors $a, b, c$ can be expressed as.

A = [a b c]

The volume by the three basis vectors is given as $ϵ^{3}$ or $| e |^{3}$

The determinant, measures ratio between the initial volume of three basis vectors, and its final volume after being scaled by $A$ .

det (A) = (a \times b) \cdot c

where $(a \times b) \cdot c$ is the volume of the cuboid.

det (A) = c_{1} (a_{2} b_{3} - b_{2} a_{3}) - c_{2} (a_{1} b_{3} - b_{1} a_{3}) + c_{3} (a_{1} b_{2} - b_{1} a_{2})

Fun fact

\vec{a} \times \vec{b} = det (\begin{matrix} i & a_{1} & b_{1} \\ j & a_{2} & b_{2} \\ k & a_{3} & c_{3} \end{matrix})

The determinant tells us about the invertibility of the Matrix

Eigenvector and Eigenvalue

An eigenvector of a matrix is a nonzero vector that, when the matrix is applied to it, is scaled by a factor $λ$ (the eigenvalue) but does not change direction.

\begin{aligned} A v & = λ v \\ A v - λ v & = 0 \\ (A - λ I) v & = 0 \end{aligned}

A linear system $M x = 0$ has non zero solution of $x$ if $det (M) = 0$ . (Suggesting that M is singular).

Thus to find non zero solution of $v$ .

det (A - λ I) = 0

Solving for $λ$ would allow us to solve for eigenvector $v$ .

Linear Algebra (Modern)

Infinite Vectors and Functional Spaces

"The only thing limiting us in Math is our imagination" ~ Joshua

Functions are vectors. What? Yes it's true. All functions are an infinite vector and these infinite vectors live within something called a Functional Space.

Introduction to Infinite-dimensional vectors functions

Take a function $f (x)$ . Suppose we get all values of $f (x)$ from $0 \leq x \leq n$ . And formulate them in a vector.

f (x) = (\begin{matrix} f (0) \\ f (0.00 \dots 1) \\ ⋮ \\ f (n) \end{matrix})

Orthogonal Basis

Suppose $f (x) = \sin x$ . Since $\sin$ is an oscillatory function, the domain of $x$ that we are interested in is thus $x \in {R | 0 \leq x \leq 2 π}$

Recall that in Euclidean space, a linear combination of two orthogonal (perpendicular) vectors, $\hat{i}$ and $\hat{j}$ can describe any point on the plane? Similarly, to describe any point/functions within this Functional space, we want to find orthogonal vectors or functions.

Thus we need to find two functions where its dot product is 0.

\hat{f} (x) \cdot \hat{g} (x) = 0

When dealing with finite vectors, the dot product is defined as such, where each element in the vector is multiplied and summed together.

\hat{A} \cdot \hat{B} = \sum_{n = 1} a_{n} b_{n}

Similarly, in the context of infinite vectors, it is defined as

\hat{f} (x) \cdot \hat{g} (x) = \int f (x) g (x) d x

Fourier discovered that the two functions $f (x)$ and $g (x)$ are $\sin x$ and $\cos x$ respectively. As

\int_{0}^{2 π} \sin x \cos x d x = 0

Thus, $\sin$ and $\cos$ act as orthogonal basis vectors in Functional space. Proving that every single function can be expressed as a linear combination of $\sin$ and $\cos$ waves.

References

https://www.youtube.com/watch?v=dT30kLnQNUE

Linear Algebra (Elementary)

Vectors

Dot Product

Cross Product

Area bounded by Vectors

Points, Lines, Planes

Point

Lines

Distance between Point and Line

Planes

Line of Intersection between two planes

Intersection of Planes

Distinguishing between no solutions & Infinite solutions

Distance between two parallel planes

Linearity

Matrices

Matrix Multiplication (How does it transform between x^ to y^?)

System of Linear Equations

Transpose

Determinant

Eigenvector and Eigenvalue

Linear Algebra (Modern)

Infinite Vectors and Functional Spaces

Introduction to Infinite-dimensional vectors functions

Orthogonal Basis

References

Matrix Multiplication (How does it transform between $\hat{x}$ to $\hat{y}$ ?)