Distributions

It is highly recommended to read Probability beforehand.

Binomial Distribution

This section handles the instance where a choice between two options has to be made. We can visualise it as a probability tree

Problem

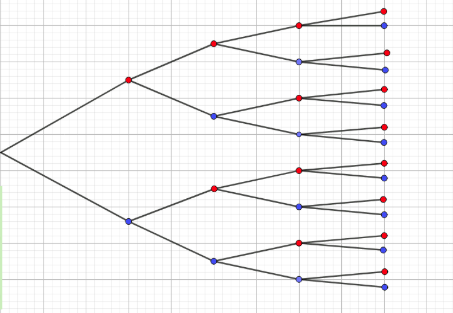
Suppose there is an equal probability to get a red or blue ball. What is the probability that red has been picked at least 2 times.

P (R \geq 2) = \frac{1}{2^{4}} \cdot [(\binom{4}{4}) + (\binom{4}{3}) + (\binom{4}{2})]

There are 4C4 ways to pick 4 reds, 4C3 to pick 3 and 4C2 ways to pick 2. The total number of possible outcomes is also $2^{4}$ . (recall permutations)

Problem

If the probability of getting a red ball is $0.7$ , what is the probability that red has been picked exactly twice?

P (R = 2) = (\binom{4}{2}) \cdot {0.7}^{2} \cdot {0.3}^{2}

The probability of traversing down a single path on the tree with 2 red balls is ${0.7}^{2} \cdot {0.3}^{2}$ . Since there are 4C2 paths with 2 red balls. We sum the total probability by multiplying the two together. We can rewrite the above for any value of red balls $(r)$ and tries $(n)$ as.

P (R = r) = (\binom{n}{r}) p^{r} (1 - p)^{n - r}

Thus we say that R follows a binomial distribution.

R \sim Bin (n, p)

If you were to plot $P (R = r)$ against $r$ for large values of $n$ . You'll get a smooth bell shaped curve called the binomial distribution.

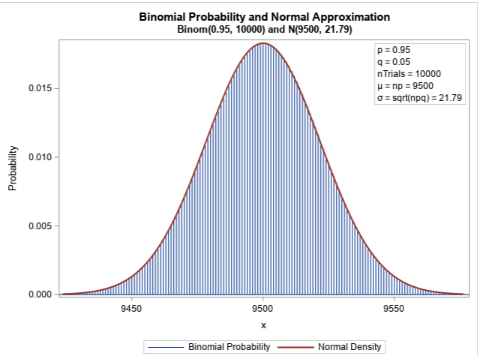
Above shows a binomial distribution where $n = 1000$ and $p = 0.95$ .

Quiz

A Galton board consist of a narrow opening at the top which allows holes to fall through a series of pins before dropping into a bin at the bottom. Can you explain what distribution the balls will follow and why?

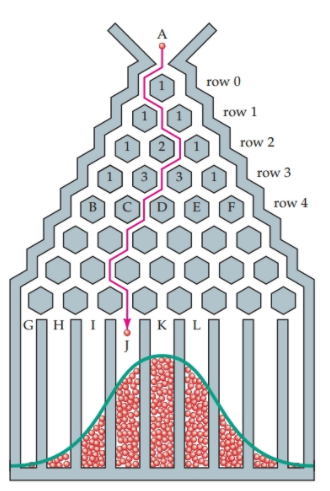
Ans:
For a ball to fall into pocket J, it chooses to move left or right 8 times. The number of times it moved left is 5 times, and right is 3 times. Since there is an equal possibility of moving left or right, $p = 0.5$ .

Thus, there are 8C5 paths that reaches pocket J. And the probability of each individual path is ${0.5}^{8}$ .

P (X = J) = (\binom{8}{5}) (0.5)^{8}

Extending this to all the other pockets. where $x$ is the number of times the ball has to turn left or right to reach the pocket.

P (X = x) = (\binom{n}{x}) (0.5)^{8}

We see that this $P (X = x)$ is a binomial distribution, where $x$ denotes the final position of the ball. Thus, the ball should follow a binomial distribution.

X \sim Bin (8, 0.5)

Normal Distribution

Central Limit Theorem

The CLT states that the summation of independent random processes always follow a Normal distribution. Binomial distribution is just a variant of a Normal distribution.

X \sim N (μ, σ^{2})

where $μ$ is the mean, and $σ$ is the standard deviation, and $σ^{2}$ is the variance

The probability of observing X is given as

f_{X} (x) = \frac{1}{σ \sqrt{2 π}} e^{- \frac{1}{2} {(\frac{x - μ}{σ})}^{2}}

The Gaussian Distribution is given as

\frac{1}{σ \sqrt{2 π}} e^{- \frac{1}{2} {(\frac{x - μ}{σ})}^{2}}

But for the sake of our sanity, lets just ignore all this and reduce the formula to the below. Basically all normal distributions are usually in this form

e^{- x^{2}}

Fun fact

Do you know that the expression below simply cannot be defined using known identities? (No arrangement of $\sin, \cos, \ln e t c$ can arrive at the solution).

\int e^{- x^{2}} d x

But Mathematicians were able to figure out that (proof) Its a really beautiful proof (Go check it out)

\int_{- \infty}^{\infty} e^{- x^{2}} d x = \sqrt{π}