Combinations and Permutations

Combinations

There are $n!$ ways to rearrange $n$ distinct objects.

n! = n \cdot (n - 1) \cdot (n - 2) \dots \cdot

There are $(\binom{n}{r})$ ways to pick $r$ objects from $n$ objects

(\binom{n}{r}) = \frac{n!}{r! (n - r)!}

why tho?

Suppose we have 5 objects (ABCDE), and want to find the number of ways to pick 2 objects such as AB or AD.... There are $5!$ ways to rearrange ABCDE like BACDE or CABDE. Suppose we only look at the first two letters in this $5!$ different combinations.

Combinations of ABCDE	First two letters
ABCDE	AB
ABDCE	AB
ABEDC	AB
ABECD	AB
ABDEC	AB
ABCED	AB
...	...

We see that the first two letters repeat six times. Pay special attention to the last 3 letters. Notice that we go through all $3!$ or $(n - r)!$ possible arrangements of C, D & E? Thus, since AB are all repeated, we divide $5!$ or $n!$ by $(n - 2)! = 3!$ to get $\frac{5!}{3!}$ .
However, we still have not accounted for the shuffling of A & B

Combinations of ABCD	First two letters
ABCDE	AB
BACDE	BA

As Combinations do not care about order, AB and BA are equivalent or repeated. Since there are $r!$ or $2!$ ways to rearrange 2 letters. We divide $\frac{5!}{3!}$ by $2!$

Thus the total number of ways to pick 2 objects from 5 objects is $\frac{5!}{3! 2!}$

Permutations

How many ways can you pick and arrange $r$ objects from $n$ objects.

^{n} P_{r} = \frac{n!}{(n - r)!}

In permutation, order matters. For example, given 3 choices (ABC) and pick two. $(\binom{3}{2})$ would only find 3 ways, AB, BC, AC. However, $^{3} P_{2}$ will find 6 ways, AB, BA, BC, CB, AC, CA. (NOTE: order matters)

Thus, hopefully you can understand why the formula works, given the above explanation for combinations.

Problem #1

John is trying to set up a 6 digit password. Given that he has 12 numeric characters, How many permutations of his passwords are there?

Ans: $12^{6}$ permutations.

Problem #2

How many different path can be made from point A to B, without passing through C.

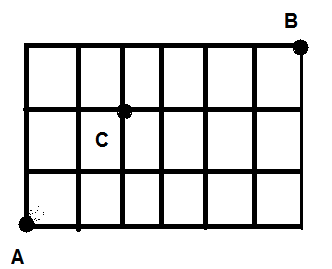
Ans:
There are 9 moves to make, you have to move up (U) 3 times, and right (R) 6 times to reach from A to B. Thus the number of ways to reach from A to B is the number of ways you can choose 3 of the moves to be up, which is $(\binom{9}{3})$ .

The number of ways to go from A to C is $(\binom{4}{2})$ and from C to B is $(\binom{5}{1})$
Thus, the total number of ways to move from A to B, while passing through C is $(\binom{4}{2}) \cdot (\binom{5}{1})$ .

Thus the answer is

(\binom{9}{3}) - (\binom{4}{2}) \cdot (\binom{5}{1}) = 54