Algebra

Algebra has evolved throughout the century. Since the invention of group theory, it has evolved from elementary to modern Algebra.

What is Algebra?

Algebra is the branch of mathematics that studies structures, relationships, and operations on symbols and sets, using rules to solve equations, analyze patterns, and explore abstract systems like groups, rings, and fields.

Elementary Algebra

Fundamental Theory of Elementary Algebra

Every polynomial that has complex coefficients is guaranteed to have at least one complex root.

Functions

A function receives an input and produces an output.

f : R \mapsto R

The function $f (x)$ maps an element from
$R$ to another element in $R$

For example, suppose $x \in R$

f (x) = y

Where $y \in R$ . We can see $f : x \mapsto y$

Injective, Bijective, Surjective

The way in which f maps from A to B can be categorised in three categories. Injective, Surjective and Bijective.

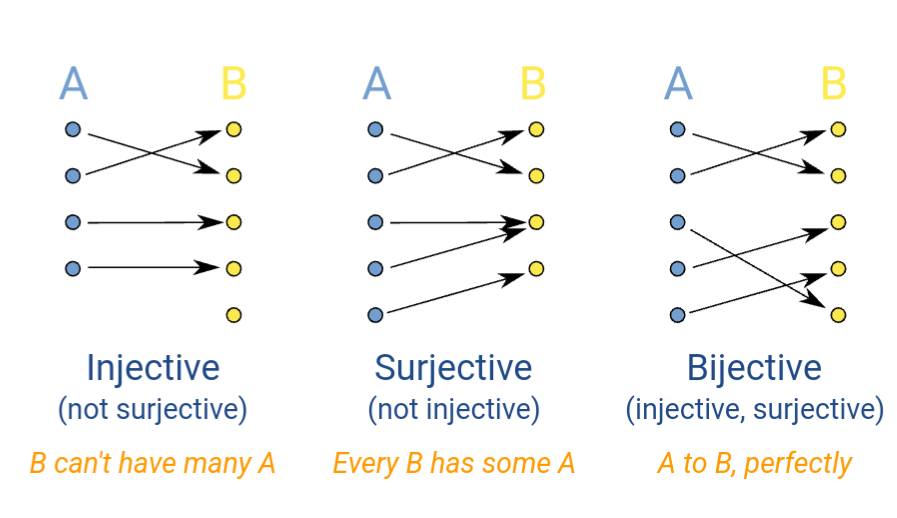
If a function is Bijective, it has an inverse.

Univariable Functions

Completing the Square

x^{2} \pm k x + c = (x \pm \frac{k}{2})^{2} - \frac{k^{2}}{4} + c

Sum and Products of roots

f (x) = u_{n} x^{n} + u_{n - 1} x^{n - 1} \dots

let $r$ be the set of roots of $f (x)$ .

f (α) = 0, \forall α \in r

Sum of roots

\sum α = - \frac{u_{n - 1}}{u_{n}}

Product of roots

\prod α = (- 1)^{n} \frac{u_{0}}{u_{n}}

Composite Functions

f (g (x)) = (f \circ g) (x)

f^{- 1} \circ g^{- 1} (x) = (g \circ f)^{- 1} (x)

f \circ f^{- 1} (x) = f^{- 1} \circ f (x) = x